The formula of a compound provides essential information about the elements it contains and the ratio in which they are present. There are two main types of chemical formulae used to describe the composition of a molecule: the empirical formula and the molecular formula.
Defining Chemical Formulae
Understanding the distinction between an empirical and a molecular formula is crucial for interpreting chemical information and solving stoichiometric problems.
- An empirical formula represents the simplest whole-number ratio of atoms of each element present in a compound.
- A molecular formula shows the actual number of atoms of each element in one molecule of a compound.
For some compounds, like water (H₂O), the empirical and molecular formulae are the same. For many others, especially organic compounds, they are different.
Comparison of Empirical and Molecular Formulae
| Feature | Empirical Formula | Molecular Formula |
| Information Provided | The simplest ratio of elements. | The actual number of atoms per molecule. |
| Uniqueness | Can be the same for different compounds (e.g., CH₂ is the empirical formula for ethene, propene, and butene). | Unique to a specific compound. |
| Example (Ethene) | CH₂ | C₂H₄ |
| Example (Glucose) | CH₂O | C₆H₁₂O₆ |
| Example (Water) | H₂O | H₂O |
Calculating the Empirical Formula
The empirical formula can be determined from experimental data, either from the percentage composition by mass of the elements in a compound or from the masses of elements in a known sample.
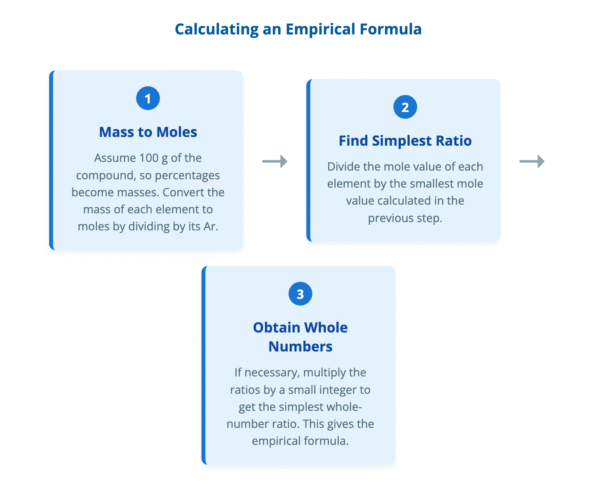
The calculation follows a clear, three-step process:
- Mass to Moles: Convert the mass (or percentage) of each element into an amount in moles by dividing by its relative atomic mass (Ar).
- Find Simplest Ratio: Divide the mole value for each element by the smallest mole value calculated in step 1.
- Obtain Whole Numbers: If the results from step 2 are not whole numbers, multiply all the values by a small integer (usually 2 or 3) to obtain the simplest whole-number ratio.
Example Calculation from Percentage Composition
A compound contains 85.7% carbon and 14.3% hydrogen by mass. Determine its empirical formula.
(Ar values: C = 12.0, H = 1.0)
| Carbon (C) | Hydrogen (H) | |
| Step 1: Moles | 85.7 / 12.0 = 7.142 | 14.3 / 1.0 = 14.3 |
| Step 2: Ratio | 7.142 / 7.142 = 1 | 14.3 / 7.142 = 2 |
The simplest ratio of C:H is 1:2. The empirical formula is CH₂.
Example Calculation from Reacting Masses
When 1.55 g of phosphorus is completely combusted, 3.55 g of an oxide of phosphorus is produced. Deduce the empirical formula of the oxide.
(Ar values: P = 31.0, O = 16.0)
- Mass of Phosphorus = 1.55 g
- Mass of Oxygen = Total mass of oxide – Mass of phosphorus = 3.55 g – 1.55 g = 2.00 g
| Phosphorus (P) | Oxygen (O) | |
| Step 1: Moles | 1.55 / 31.0 = 0.0500 | 2.00 / 16.0 = 0.125 |
| Step 2: Ratio | 0.0500 / 0.0500 = 1 | 0.125 / 0.0500 = 2.5 |
| Step 3: Whole Numbers | 1 × 2 = 2 | 2.5 × 2 = 5 |
The simplest whole-number ratio of P:O is 2:5. The empirical formula is P₂O₅.
Determining the Molecular Formula
The molecular formula is always a whole-number multiple of the empirical formula. To determine the molecular formula, two pieces of information are required:
- The empirical formula of the compound.
- The relative molecular mass (Mr) of the compound.
Example Calculation
A compound has the empirical formula CH₂Br. Its relative molecular mass is 187.8. Deduce the molecular formula.
(Ar values: C = 12.0, H = 1.0, Br = 79.9)
- Calculate the empirical formula mass:
Mass of CH₂Br = 12.0 + (2 × 1.0) + 79.9 = 93.9 - Find the multiplier:
Multiplier (n) = Relative molecular mass / Empirical formula mass
n = 187.8 / 93.9 = 2
Determine the molecular formula:
Molecular Formula = (Empirical Formula)ₙ = (CH₂Br)₂ = C₂H₄Br₂
