The Molar Volume of a Gas
Avogadro’s hypothesis states that equal volumes of any gas, measured under the same conditions of temperature and pressure, contain an equal number of molecules. This principle allows us to relate the volume of a gas directly to the number of moles present.
The molar gas volume is the volume occupied by one mole of any gas. At room temperature and pressure (r.t.p.), which is defined as approximately 20 °C and 1 atmosphere, the molar gas volume is 24.0 dm³ mol⁻¹.
This means that 24.0 dm³ of carbon dioxide, 24.0 dm³ of hydrogen, or 24.0 dm³ of any other gas at r.t.p. all contain exactly one mole of gas molecules.
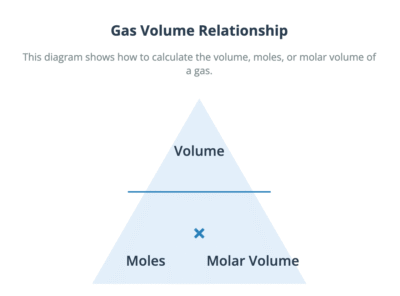
Calculations Using Molar Gas Volume at r.t.p.
The relationship between the number of moles and the volume of a gas at r.t.p. can be expressed with two key formulas. These are fundamental for calculations involving gas volumes.
To find the volume of a gas from a known number of moles:
Volume of gas (in dm³) = Number of moles × 24.0
To find the number of moles of a gas from a known volume:
Number of moles = Volume of gas (in dm³) / 24.0
Example Calculation 1: Finding Volume from Mass
Calculate the volume occupied by 13.2 g of carbon dioxide gas, CO₂, at r.t.p.
(Aᵣ values: C = 12.0, O = 16.0)
Step 1: Calculate the molar mass of CO₂.
Molar mass = 12.0 + (2 × 16.0) = 44.0 g mol⁻¹
Step 2: Calculate the number of moles of CO₂.
Number of moles = Mass / Molar mass = 13.2 g / 44.0 g mol⁻¹ = 0.300 mol
Step 3: Calculate the volume of the gas.
Volume = Number of moles × 24.0 dm³ mol⁻¹ = 0.300 mol × 24.0 dm³ mol⁻¹ = 7.20 dm³
Example Calculation 2: Finding Mass from Volume
Calculate the mass of 180 cm³ of methane gas, CH₄, at r.t.p.
(Aᵣ values: C = 12.0, H = 1.0)
Step 1: Convert the volume to dm³.
Volume in dm³ = 180 cm³ / 1000 = 0.180 dm³
Step 2: Calculate the number of moles of CH₄.
Number of moles = Volume / 24.0 dm³ mol⁻¹ = 0.180 dm³ / 24.0 dm³ mol⁻¹ = 0.00750 mol
Step 3: Calculate the molar mass of CH₄.
Molar mass = 12.0 + (4 × 1.0) = 16.0 g mol⁻¹
Step 4: Calculate the mass of the gas.
Mass = Number of moles × Molar mass = 0.00750 mol × 16.0 g mol⁻¹ = 0.120 g
Gas Volumes and Stoichiometry
According to Avogadro’s hypothesis, the mole ratio in a balanced chemical equation is equivalent to the volume ratio for reacting gases, provided the volumes are measured at the same temperature and pressure. This allows for direct stoichiometric calculations involving gas volumes.
For example, in the synthesis of ammonia:
N₂(g) + 3H₂(g) → 2NH₃(g)
The mole ratio is 1 : 3 : 2.
This means that 1 volume of nitrogen reacts with 3 volumes of hydrogen to produce 2 volumes of ammonia. For instance, 10 cm³ of N₂ will react exactly with 30 cm³ of H₂ to produce 20 cm³ of NH₃.
Example Calculation 3: Deducing a Molecular Formula
When 40 cm³ of a gaseous hydrocarbon was completely combusted with 240 cm³ of oxygen (an excess), the resulting gas mixture had a volume of 200 cm³ after cooling. After passing this mixture through aqueous sodium hydroxide, the volume reduced to 80 cm³. All volumes were measured at r.t.p. Deduce the molecular formula of the hydrocarbon.
Step 1: Determine the volume of products.
The contraction in volume when passed through NaOH is due to the removal of CO₂.
Volume of CO₂ produced = 200 cm³ – 80 cm³ = 120 cm³
The remaining 80 cm³ must be the excess, unreacted oxygen.
Step 2: Determine the volume of oxygen that reacted.
Volume of O₂ reacted = Initial volume of O₂ – Excess volume of O₂
Volume of O₂ reacted = 240 cm³ – 80 cm³ = 160 cm³
Step 3: Find the simplest whole number ratio of reacting volumes.
Let the hydrocarbon be CₓHᵧ.
CₓHᵧ(g) + O₂(g) → CO₂(g)
Reacting volumes: 40 cm³ : 160 cm³ : 120 cm³
Simplest ratio: 1 : 4 : 3
Step 4: Use the ratios to find x and y.
From the ratio, the balanced equation starts:
1CₓHᵧ(g) + 4O₂(g) → 3CO₂(g) + zH₂O(l)
From balancing the carbon atoms: x = 3.
From balancing the oxygen atoms:
Total oxygen on left = 4 × 2 = 8 atoms.
Oxygen in CO₂ = 3 × 2 = 6 atoms.
Therefore, oxygen atoms in water = 8 – 6 = 2 atoms. This means z = 2.
1C₃Hᵧ(g) + 4O₂(g) → 3CO₂(g) + 2H₂O(l)
From balancing the hydrogen atoms: y = 2 × 2 = 4.
The molecular formula of the hydrocarbon is C₃H₄.
