Angular velocity is the rate at which an object rotates or revolves about an axis, measured as the change in angular displacement over a period of time.

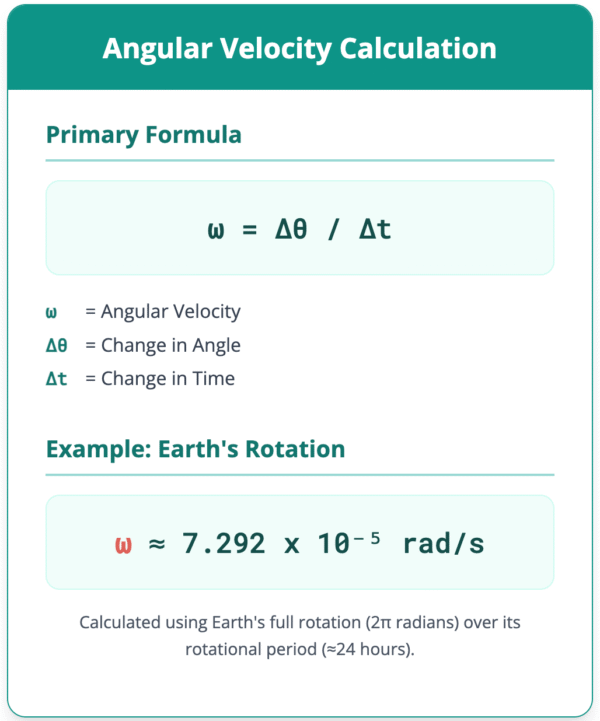
To calculate it, the primary formula used is ω = Δθ / Δt, where ω is the angular velocity, Δθ is the change in angle, and Δt is the change in time. The angular velocity of Earth, with respect to its own rotational axis, is calculated by considering its full rotation of 2π radians over a period of approximately 24 hours.

This calculation yields a constant value of approximately 7.292 x 10⁻⁵ radians per second for any point on the planet’s surface.

Fundamental Concepts of Angular Velocity

In physics, motion is not limited to linear travel; objects also rotate. Angular velocity is the fundamental measure used to describe this rotational motion.

Defining Angular Velocity

Angular velocity, represented by the Greek letter omega (ω), is a vector quantity that specifies the rotational speed of an object and the direction of its spin. In simpler terms, it answers the question: “How fast is it turning?” The standard unit for measuring angular velocity is radians per second (rad/s), as radians provide a direct mathematical link between angular and linear motion.

The Relationship with Linear Velocity

It is important to distinguish angular velocity from linear velocity. While angular velocity describes the rate of rotation for the entire rigid object, linear velocity (v) describes how fast a single point on that object is moving along its circular path. A point farther from the center of rotation moves faster (has a higher linear velocity) than a point closer to the center, even though both have the same angular velocity. The relationship is given by the formula v = rω, where r is the radius from the axis of rotation.

How to Calculate Angular Velocity

There are several standard formulas used to determine the angular velocity of an object, depending on the information available.

The Primary Formula

The most direct way to calculate angular velocity is by measuring the change in angle over time. This provides the average angular velocity over that interval.

The formula is:

ω = Δθ / Δt

• ω is the angular velocity.
• Δθ (delta theta) is the angular displacement, or the change in the angle of the object.
• Δt (delta t) is the time interval over which the angle changes.

Calculation Using Frequency or Period

In many physical systems, rotation is cyclical. In such cases, angular velocity can be calculated from two related properties: period and frequency.

• Period (T): The time it takes to complete one full revolution (2π radians). The formula is ω = 2π / T.
• Frequency (f): The number of revolutions completed per unit of time. The formula is ω = 2πf.

Calculating the Angular Velocity of Earth

The rotation of the Earth on its axis is a classic example of angular velocity. Because the Earth rotates as a rigid body, every point on its surface—from the equator to the poles—completes one full circle in the same amount of time, and thus shares the same angular velocity.

The Earth’s Rotational Parameters

To perform the calculation, we use the known rotational period of the planet.

• The angular displacement (Δθ) for one complete rotation is 360 degrees, which is equivalent to 2π radians.
• The time interval (Δt), known as the sidereal day, is the time it takes for the Earth to rotate 360 degrees relative to the stars. This period is approximately 23 hours, 56 minutes, and 4.1 seconds.

Step-by-Step Calculation

Using these values, we can calculate the angular velocity of Earth.

1. Convert the period (T) into seconds.
   T = (23 hours × 3600 s/hr) + (56 min × 60 s/min) + 4.1 s = 82800 + 3360 + 4.1 = 86,164.1 seconds.
2. Identify the angular displacement (Δθ).
   For one full rotation, Δθ = 2π radians.
3. Apply the formula using the period.
   ω = 2π / T
4. Substitute the values and calculate.
   ω = 2π / 86,164.1 s ≈ 7.2921 x 10⁻⁵ rad/s

For most general applications, using an approximation of 24 hours (86,400 seconds) is common, which yields a very close value of 7.272 x 10⁻⁵ rad/s.

Frequently Asked Questions

What is the difference between angular velocity and angular speed?

Angular speed is the magnitude (the numerical value) of the angular velocity. Angular velocity is a vector, meaning it also has a direction, which is typically described by the right-hand rule along the axis of rotation. For many calculations, the terms are used interchangeably when only the rate of rotation is considered.

Is the Earth’s angular velocity constant everywhere on its surface?

Yes. Since the Earth rotates as a single rigid body, every point completes a 360-degree turn in the same amount of time. Therefore, the angular velocity is the same whether you are at the equator or near one of the poles. However, the linear velocity is greatest at the equator and zero at the poles.

How does the Earth’s angular velocity affect us?

The Earth’s rotation creates the Coriolis effect, an inertial force that deflects moving objects (like air currents, ocean currents, and projectiles) to the right in the Northern Hemisphere and to the left in the Southern Hemisphere.

• Percent Deviation Calculator
• Turning Radius Calculator

Related